オームの法則をマスターしよう！【中２理科】

抵抗に流れる電流とかかる電圧の関係

電線に乗っているカラスをみたことがありますよね。

あのカラスは電線の電気で感電カラスにならないんでしょうか？

カラスが両足で電線に止まっている時、カラスの右足と左足と電線で１つの回路ができて、カラスの体を電流が流れて感電してしまいそうなものですが、なぜ感電しないのでしょうか？

これには、物質の電流の流れやすさが関係しています。

カラスの体よりも電線のほうが圧倒的に電流が流れやすいんです。そのためカラスの体には電流はほとんど流れないというわけです。

このように物質ごとに電流の流れにくさが決まっていて、この電流の流れにくさのことを抵抗といいます。

抵抗の単位はΩ（オーム）といい、この値が大きいほど電流が流れにくくなります。

電圧と電流にはどんな関係があるのでしょうか？

今回は抵抗を使って電圧と電流の関係を解明していきましょう！

「電圧」と「電流」と「抵抗」３つの関係

抵抗に電圧をかけて流れる電流を調べてみましょう。

注意点として、電源装置には電圧と電流が表示されていますが、実験では電圧計と電流計の両方を使っています。

理由は電源装置に表示されている値は「電源装置に」かかる電圧と電流なので、導線に電圧がかかったりと抵抗の値と少しずれてしまうから電源装置に表示されている値は使わないんですね。

早速10Ωの抵抗を使って、回路を作って測定します。

今回は電流計と電圧計の２つを回路に組み込みます。電流計は直列つなぎ、電圧計は並列つなぎでしたね。

電源装置と抵抗ををつなげて電圧をかけて実験をしてみると、電源の電圧を1Vにした時、抵抗に100mAの電流が流れました。

このようにして電圧の値を変えながら抵抗を流れる電流の大きさを測定します。

すると結果は

このようになりました。

電圧の大きさと流れる電流の大きさは比例していることがわかりますね。

上の実験は同じ抵抗を使って、「電圧」の値を変えましたが、次に「抵抗」の値を変えて実験してみましょう。

次の実験は電圧の大きさを６Vに固定して、10Ω、20Ω、30Ωの３つの抵抗に変えて流れる電流の大きさを測ってみます。

結果は

となりました。

この結果からは抵抗の大きさと電流の大きさは反比例の関係にあることがわかります。

２つの実験結果から

・電圧と電流は比例

・抵抗と電流は反比例

ということがわかりました。

この２つの実験結果から「電圧」と「電流」と「抵抗」の３つを入れた式を考えてみましょう。

数学の一次関数の授業で習ったことを使うと、比例しているｘとｙはｙ＝aｘという式で表されました。

つまり電圧と電流は比例しているので、$V＝a×I（aは比例定数）$となります。

反比例の場合は難しいですが、a＝ｘ×ｙの形で表されます。（数学の授業ででてきますがちょっと難しいのでわからない場合は飛ばしてね）

抵抗と電流が反比例なので、a＝Ω×Iとなります。

今できた２つの式を合わせると

$V（電圧）=R（抵抗）×I（電流）$

という式が出来上がります！

この式を使うと電圧、電流、抵抗の３つの関係が一瞬でわかります。

この公式をオームの法則といいます。

ここから記号がたくさんでてくるので、こんがらがってしまわないように記号と単位の復習をしましょう！

式で書く時は記号で書いて、答えに単位が付きます。紛らわしいですが、式と答えの違いに注目して考えましょう！

ちなみに、オームは元々アルファベットのＯを使ってましたが、ゼロ0と紛らわしいのでギリシャ文字のオメガΩが使われるようになりました。

オームの法則の計算式を使えば、実験で測った値から抵抗に流れる電流とかけた電圧から抵抗の大きさが分かります。

実際に計算問題に挑戦してみましょう。

オームの法則の計算

さてオームの法則の式にもどると

$V（電圧）=R（抵抗）×I（電流）$

でした。

実験で求められた10Ωの抵抗に６Vの電圧をかけたときの電流は600ｍAでした。

オームの法則の式に代入してみましょう。

オームの法則を使う時はｍＡではなく、Aを使わないといけません。

なので、600ｍAを0.6Aにして計算します。

$6V＝10Ω×0.6A$となりました。

どうやら合っていそうですね！

計算問題

少し計算問題に挑戦していきましょう！

問題１

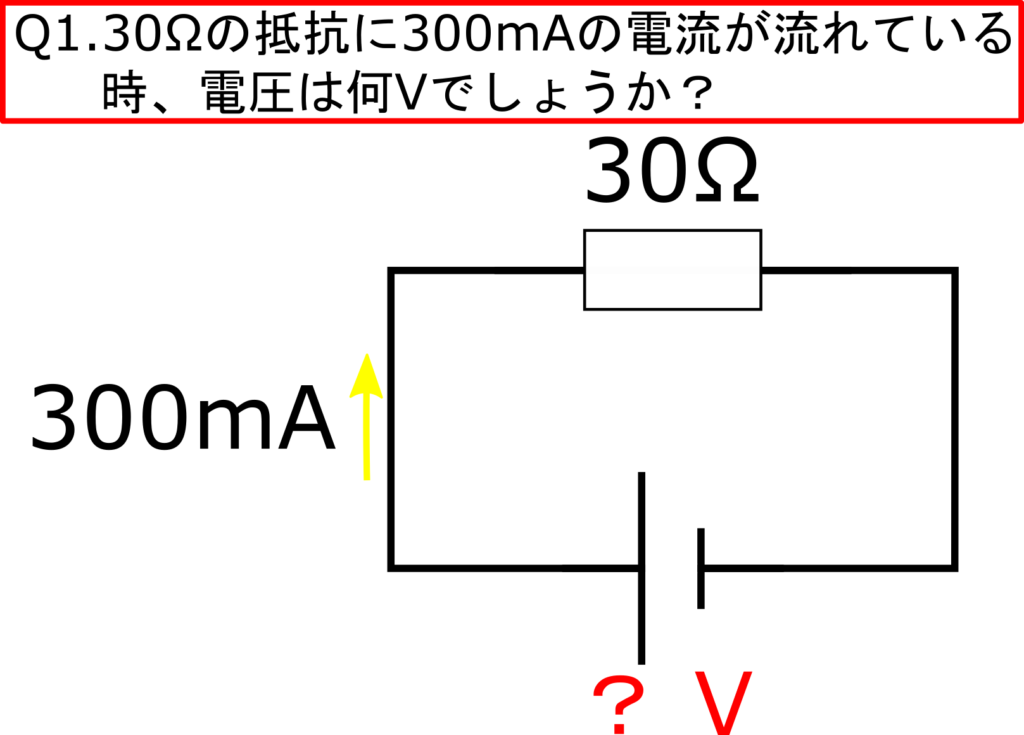
式に当てはめて計算してみましょう。

まず、300ｍA＝0.3Aに変換します。そして式に代入します。

$V＝30Ω×0.3A＝9V$

簡単ですね！

次の問題に行きましょう！

問題２

今回はアンペアを求める問題です。

なので式の変形をしていきましょう！

A＝の形にしたいので、右辺のRを消すために両辺をRで割ります

$V÷R＝R×A÷R$

$\cfrac{V}{R}=A$

右辺と左辺を入れ替えると

$A=\cfrac{V}{R}$

となりますね。この式に問題の数値を代入して電流の大きさを求めてみましょう。

問題文にある20Ωと4Vの条件を代入して

$A=\cfrac{4V}{20Ω}=0.2A$

となります。

最後に抵抗を求める問題にも挑戦してみましょう！

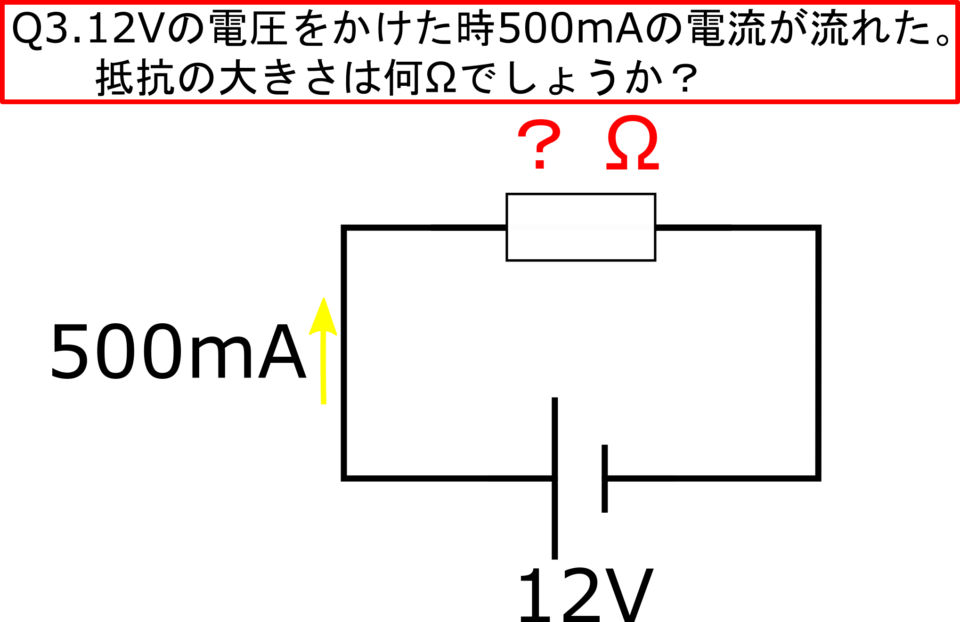
問題３

Q2と同じように式をRを求める形に変形しましょう！

$V（電圧）=R（抵抗）×I（電流）$

この式の両辺をIで割ると

$V÷I＝R×I÷I$

となって、$\cfrac{V}{I}=R$

右辺と左辺を入れ替えて$R=\cfrac{V}{I}$

となりますね。

値を代入すると

$R=\cfrac{12V}{0.5A}=24Ω$

となります。

これで完璧ですね！

オームの法則の式をまとめるとこんな感じです！

ぜひこの３つの式を覚えて計算をマスターしてください！

次の学習

あわせて読みたい

オームの法則を使って合成抵抗の大きさを求めよう【式がわかれば完璧】 【豆電球の明るさの秘密】 クリスマスツリーのライトって、１つだけ切れているのはなかなかなくて、そのあたりが連鎖して切れています。ということは、そのライトは並列...

関連記事

あわせて読みたい

直列回路は電流が等しく・並列回路は電圧が等しくなる理由を徹底解説！！ 【電流と電圧の不思議な関係】 今までの学習で電流と電圧の関係がわかってきたと思います。 なんとなく電源からかかる電圧が大きければ電流も大きくなるような気がしま...